beta distribution r|fit beta distribution in r : Bacolod Compute the first four ordinary moments, central moments, mean, variance, Pearson's coefficient of skewness, kurtosis, coefficient of variation, median and quartile deviation . When the printer list appears, select Update from the View menu. After a few moments, the printer list will be updated and the printer you configured for wireless use will now show in the list that it is connected to your wireless network. The printer is connected to your wireless network.
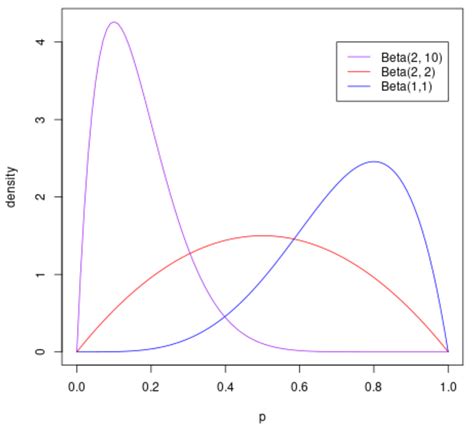
beta distribution r,Beta distribution is one type of probability distribution that represents all the possible outcomes of the dataset. Beta distribution basically shows the probability of probabilities, where α and β, can take .The Beta Distribution. Description. Density, distribution function, quantile function and random generation for the Beta distribution with parameters shape1 and shape2 (and .The Beta Distribution Description. Density, distribution function, quantile function and random generation for the Beta distribution with parameters shape1 and shape2 (and .
Compute the first four ordinary moments, central moments, mean, variance, Pearson's coefficient of skewness, kurtosis, coefficient of variation, median and quartile deviation .beta distribution rThe Beta Distribution. Description. Density, distribution function, quantile function and random generation for the Beta distribution with parameters shape1 and shape2 (and .In R, you can generate random numbers from a beta distribution using the rbeta() function and plot the probability density function (PDF) or cumulative distribution function (CDF) using the dbeta() and pbeta() functions, .The beta distribution. Description. Density, distribution function, quantile function and random number generation for the beta distribution with parameters mean and sd OR .Given a vector of values, calculates the shape parameters required to produce a two-parameter Beta distribution with the same mean and variance (i.e., the first two . dgamma: This function returns the corresponding gamma density values for a vector of quantiles. The syntax in R is dgamma (x, alpha, rate = 1/beta), which takes the following arguments. x: vector of quantiles. alpha, beta: parameters of the gamma distribution. rate: an alternative way to specify the scale.The Beta distribution with parameters shape1 = a = a and shape2 = b = b has density. f (x) = Γ(a)Γ(b)Γ(a+b) xa−1(1−x)b−1. for a > 0 a >0, b > 0 b >0 and 0 \le x \le 1 0 ≤x ≤ 1 where the boundary values at x=0 x = 0 or x=1 x =1 are defined as by continuity (as limits). The mean is a/(a+b) a/(a+b) and the variance is ab/((a+b)^2 (a .The Beta distribution with parameters shape1 = a = a and shape2 = b = b has density. f (x) = Γ(a)Γ(b)Γ(a+b) xa−1(1−x)b−1. for a > 0 a >0, b > 0 b >0 and 0 \le x \le 1 0 ≤x ≤ 1 where the boundary values at x=0 x = 0 or x=1 x =1 are defined as by continuity (as limits). The mean is a/(a+b) a/(a+b) and the variance is ab/((a+b)^2 (a .为了具体了解R中的β分布,我们将学习β函数。 β函数 是β分布的一个组成部分(R中的β函数可以用β(a,b)函数来实现),其中包括这些beta、pbeta、qbeta和rbeta,它们是β分布的函数。 Beta函数的定义为. a=0,b=1的情况称为标准β分布。因此,标准贝塔分布是 。Johnson et.al (p.226) provides the Fisher's information matrix of the four-parameter beta distribution in the regular case where p,q > 2. Value. dBeta_ab gives the density, pBeta_ab the distribution function, qBeta_ab the quantile function, rBeta_ab generates random deviates, and eBeta_ab estimates the parameters. lBeta_ab provides the log .The generalized beta is the distribution of the random variable. where X X has a beta distribution with parameters \alpha α and \beta β . The k k th raw moment of the random variable X X is E[X^k] E [X k] and the k k th limited moment at some limit d d is E[\min(X, d)] E [min(X,d)], k > -\alpha\tau k >−ατ .
Beta Distribution in R Language is defined as property which represents the possible values of probability. This article is an illustration of dbeta, pbeta, qbeta, and rbeta functions of Beta Distribution. dbeta() Function. It is defined as Beta Density function and is used to create beta density value corresponding to the vector of quantiles.

The beta distribution for fitting a GAMLSS Description. The functions BE() and BEo() define the beta distribution, a two parameter distribution, for a gamlss.family object to be used in GAMLSS fitting using the function gamlss().BE() has mean equal to the parameter mu and sigma as scale parameter, see below.BEo() is the original parameterizations of . When the data are strictly positive and bounded then the beta distribution is often a very good choice. GLMMadaptive and glmmTMB both allow for the beta distribution. Since you seem to be familiar with glmer then glmmTMB would be the easist choice for you since all you have to do is specify family = beta_family() As for the .The beta distribution is a continuous probability distribution with two shape parameters, which is commonly used in Bayesian analysis, hypothesis testing, and modeling of proportions and rates. In R, you can generate random numbers from a beta distribution using the rbeta() function and plot the probability density function (PDF) or cumulative .in Figure 1 which depicts several different beta densities. Following Ferrari and Cribari-Neto (2004), the densities are parameterized in terms of the mean µand the precision parameter φ; all details are explained in the next section. The evident flexiblity makes the beta distribution an attractive candidate for data-driven statistical .In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or (0, 1) in terms of two positive parameters, denoted by alpha (α) and beta (β), .fit beta distribution in rDetails. The beta-binomial distribution is a binomial distribution whose probability of success is not a constant but it is generated from a beta distribution with parameters shape1 and shape2.Note that the mean of this beta distribution is mu = shape1/(shape1+shape2), which therefore is the mean or the probability of success.. .beta distribution r fit beta distribution in r The (standard) beta distribution with left parameter a ∈ (0, ∞) and right parameter b ∈ (0, ∞) has probability density function f given by f(x) = 1 B(a, b)xa − 1(1 − x)b − 1, x ∈ (0, 1) Of course, the beta function is simply the normalizing constant, so it's clear that f is a valid probability density function.mode(\theta) = \frac{\alpha - 1}{\beta +. 1} mode(θ)= β+1α−1. . The inverse-beta, also called the beta prime distribution, applies to variables that are continuous and positive. The inverse beta is the conjugate prior distribution of a parameter of a Bernoulli distribution expressed in odds. The inverse-beta distribution has also been .
Parameter (Standard) Beta Distribution. Description An implementation of the method of moments estimation of two-parameter Beta distribution param-eters. Given a vector of values, calculates the shape parameters required to produce a two-parameter Beta distribution with the same mean and variance (i.e., the first two moments) as the .

r; distributions; estimation; beta-distribution; Share. Cite. Improve this question. Follow edited Nov 29, 2017 at 17:39. Ferdi. 5,197 9 9 gold badges 46 46 silver badges 64 64 bronze badges. asked Jun 22, 2011 at 17:17. Dave Kincaid Dave Kincaid. These functions provide information about the beta binomial distribution with parameters m and s: density, cumulative distribution, quantiles, and random generation. Compared to the parameterization of 'VGAM::pbetabinom.ab', m = alpha/(alpha+beta) and s = (alpha+beta). See examples. The beta binomial .
beta distribution r|fit beta distribution in r
PH0 · r beta function
PH1 · probability distribution plot in r
PH2 · fit beta distribution in r
PH3 · beta distribution graph
PH4 · beta distribution for dummies
PH5 · beta distribution excel
PH6 · beta distribution examples
PH7 · Iba pa